Probability Of Winning Craps On First Roll
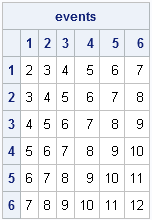
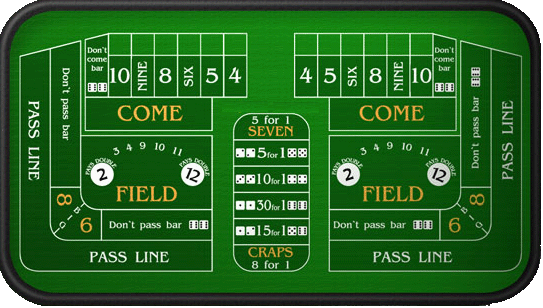
Here is an overview of craps bets with medium odds that you can make. Have a 16.7% chance of winning an Any 7 bet, with a payout of 4/1. This gives the house a substantial edge of 16.9%. This is quite high compared to some of the bets we’ve seen above, yet still a solid choice if you’re chasing more slightly more daring bets. But a come bet would have the same probability of winning as a “proper” pass line bet ( viz. 244 / 495 ≈ 0.493 ). If the point is 5 or 9, then your probability of winning would only be 0.40. And if the point is 6 or 8, then your probability of winning would only be 5 / 11 ≈ 0.45.
- Probability Of Winning Craps On First Roll Dice Game
- Probability Of Winning Craps On First Roll Hall Of Fame


Probability Of Winning Craps On First Roll Dice Game
anemone
MHB POTW Director
- Feb 14, 2012
- 3,766
Probability Of Winning Craps On First Roll Hall Of Fame
I'm aware that the
P( winning a game of craps by rolling a sum of 6)
=P(getting 6 the first time and 6 the second time) or
P(getting 6 the first time, get some number other than 6 and 7 the second time and get 6 again the third time) or
P((getting 6 the first time, get some number other than 6 and 7 the second and third time and get 6 again the fourth time)...
the sequence continues in such a manner infinitely (this is to say that we're having an infinite sum of a geometric sequence)
= $((frac{2!}{36}times2)+frac{1}{36})+ S_infty$
=$frac{5}{36}+ frac{(frac{5}{36})^2}{1-frac{25}{36}}$
=$frac{5}{36}+ frac{25}{396}$
=$frac{20}{99}$
But a quick goggle search shows that I don't have to consider the infinite sequence and the probability of winning a game of craps by rolling a sum of 6 for the third time and so on is simply
$frac{P(winning ;a ;game ;f ;craps ;by ;rolling ;a ;sum ;of ;6 }{P(winning ;or ;losing)}=frac{frac{5}{36}}{frac{5}{36}+frac{1}{36}}=frac{5}{11}$
Therefore,
P( winning a game of craps by rolling a sum of 6)
=P( winning a game of craps by rolling a sum of 6 the second time) and P(winning a game of craps by rolling a sum of 6 on the third time and so on)
=$frac{5}{36}timesfrac{5}{11}=frac{25}{369}$
Finally,
P( winning a game of craps by rolling a sum of 6)=$frac{5}{36}+ frac{25}{396}=frac{20}{99}$
I can't quite get my head around that fact. It has confused rather than enlighten me.
Could someone please explain to me why this works?
Thanks.
P( winning a game of craps by rolling a sum of 6)
=P(getting 6 the first time and 6 the second time) or
P(getting 6 the first time, get some number other than 6 and 7 the second time and get 6 again the third time) or
P((getting 6 the first time, get some number other than 6 and 7 the second and third time and get 6 again the fourth time)...
the sequence continues in such a manner infinitely (this is to say that we're having an infinite sum of a geometric sequence)
= $((frac{2!}{36}times2)+frac{1}{36})+ S_infty$
=$frac{5}{36}+ frac{(frac{5}{36})^2}{1-frac{25}{36}}$
=$frac{5}{36}+ frac{25}{396}$
=$frac{20}{99}$
But a quick goggle search shows that I don't have to consider the infinite sequence and the probability of winning a game of craps by rolling a sum of 6 for the third time and so on is simply
$frac{P(winning ;a ;game ;f ;craps ;by ;rolling ;a ;sum ;of ;6 }{P(winning ;or ;losing)}=frac{frac{5}{36}}{frac{5}{36}+frac{1}{36}}=frac{5}{11}$
Therefore,
P( winning a game of craps by rolling a sum of 6)
=P( winning a game of craps by rolling a sum of 6 the second time) and P(winning a game of craps by rolling a sum of 6 on the third time and so on)
=$frac{5}{36}timesfrac{5}{11}=frac{25}{369}$
Finally,
P( winning a game of craps by rolling a sum of 6)=$frac{5}{36}+ frac{25}{396}=frac{20}{99}$
I can't quite get my head around that fact. It has confused rather than enlighten me.
Could someone please explain to me why this works?
Thanks.