1. Probability Of Getting A Straight Flush In 5 Card Poker
2. See Full List On En.wikipedia.org

A 5-card poker hand is dealt from a well shuffled regular 52-card playing card deck. Find the probability that the hand is a Flush (5 nonconsecutive cards each of the same suit). I am completely unfamiliar with poker, and just learning the principles of probability. After the flop you've seen 4 cards of your suit, and 1 of another suit. This leaves 9 cards of your suit, and 38 of a different suit; your odds of completing your flush on the turn are thus 9/47, or 19.14%. If the turn hasn't completed your flush, your odds of completing it on the river are 9/46, or 19.5%. See full list on stattrek.com. Multiplying that by 2 gives you 18, or around an 18% chance to complete your flush on the turn. Multiplying it by 4 gets you a 36% to complete it by the river. The actual percentage odds for a flush draw hitting on the turn and then by the river are 19.1% and 35% respectively, getting you pretty close with the 2 and 4 hack.

Share

Tweet

It is a common misconception that flush is more likely to hit. If you also believe that to be the case, then you are wrong. Well, maybe you are right, but it depends on which perspective you look at it. Let me explain.

As long as you start counting the hand from preflop, then you will hit the straight more often than flush. But if you have a flush draw on flop or turn, then you will hit a flush more often compared to when you have an open-ended straight draw, and you hit a straight.

There is a reason why flush has a higher ranking in poker than straight. It will hit less often. Look at this chance to win a straight and to hit a flush – from Wikipedia.

You will hit a flush every 0.20% of the time. So once every 509 hands. While you will hit a straight about 0.40% of the time or once every 255 hands, so you will hit almost 2 straights for every 1 flush that you hit.Table of Contents

Why is it easier to make a flush than astraight?

But after all that I have written, why is it easier to hit a flush than a straight?
Well postflop, if you hold a flush draw, you have more outs to hit the draw than holding the open-ended straight draw and hitting the straight. You will have 9 outs to hit a flush on the flop or turn if you have a flush draw.
From flop to the river, we have 9 outs twice to hit a flush, which is roughly 38%, from turn to the river we have about 18% (9 outs once). On the other hand, if you hold an open-ended straight draw, you will have only 8 outs to hit it.

What many people are forgetting is that you will get the flush draw less often than you will open-ended straight draw. Getting a suited hand preflop doesn’t happen super often. You will have a flush draw on the flop only 5.1% of the time.

One thing that is often neglected is you not accounting in the times when you have a gutshot, and you hit it. It seems it doesn’t happen often, but you will usually have 4 outs to hit a straight, which is around 16% from flop to river. Not something we should forget about. On top of that, there are also some double gutters, which also gives you 8 outs to hit your straight.

So only looking from the postflop perspective, it can feel that it is easier to hit a flush than a straight, but as I explained, that can often be misleading. Straight will happen more often.

Let’s say you usually play connectors and therefore your chances to hit your straight draw increase. You would have flopped 8 outs straight draw (either open-ended or a double gutter straight draw) about 10.5% of the time on the flop.

How often will an opponent flop a flush draw?

A player will have a flush draw on the flop about 5.1% of the time strictly math speaking and accounting in all the hands. But we know that players don’t play every single hand, and they are more likely to fold more off suited hand than suited hands preflop.

All this makes an opponent hit a flush draw roughly 10% of the time on the flop.

Which makes more money: Flush vs. straight?

As expected, flush will make you more money. In my case, not double the amount, but you will make more money with it. Why not the double, you might wonder? Well, if you have a straight, usually you will be willing to stack off with top straight or second nut straight sometimes 3^rd nut straight. But when it comes to flush, you will lose quite some money even if you hold a low flush, and it can be less than 3^rd nuts. On top of that, not many players will be willing to stack off with the top two or a set on a possible flush board, while the same players don’t have a problem committing with the same hands on possible straight board.

All this reduces your winrate by a little. But you, as you can see from my graph, will still make substantially more profit with a flush compared to straight. They are both great hands; it is just that a flush is stronger.

Now your winrate will, of course, differ a bit. If you have nut flush yo will win more than my 2,000bb/100 hands. If you have a lower flush, then it will be lower. Now sometimes higher flushes will beat us. A scenario of when we hit a flush, and our opponent also hits a flush is not that uncommon, and if you multi table, it will happen on semi-frequent occasions.

The same goes for a straight. Nut straight will give you the most money of any straight. You will still make decent money with 2^nd nut straight, just less.

Scenarios, where we hit backdoor straight, will be nicely profitable since it will be harder for an opponent to put us on a straight, as there was no apparent straight draw present when we started betting on the flop. If you want to read more about straight backdoor draws, I have this article I have for you.

What are the odds of getting straight flush?

Odds of hitting a straight flush is so low that it almost doesn’t make sense to write it in percentages. It is a 0.00139% chance you will hit a straight flush. This is 72,192:1 odds against hitting it. SO only once every 72,000 hands you will hit the second most powerful hand in poker.

What are the odds of getting a royal flush?

Hitting a royal flush is even harder than a straight flush. The royal flush is the strongest hand you can get in poker. Your chances of hitting it are 0.000154% of the time, or once every650,000 hands (odds against of 649,740:1 to be precise).

I have been dealt quite many royal flushes in my poker career, and frankly, hitting one doesn’t feel special anymore. But I remember that when I hit it for the first time, I was ecstatic for some time. That is how rare the royal flush is.

Does a straight beat a flush?

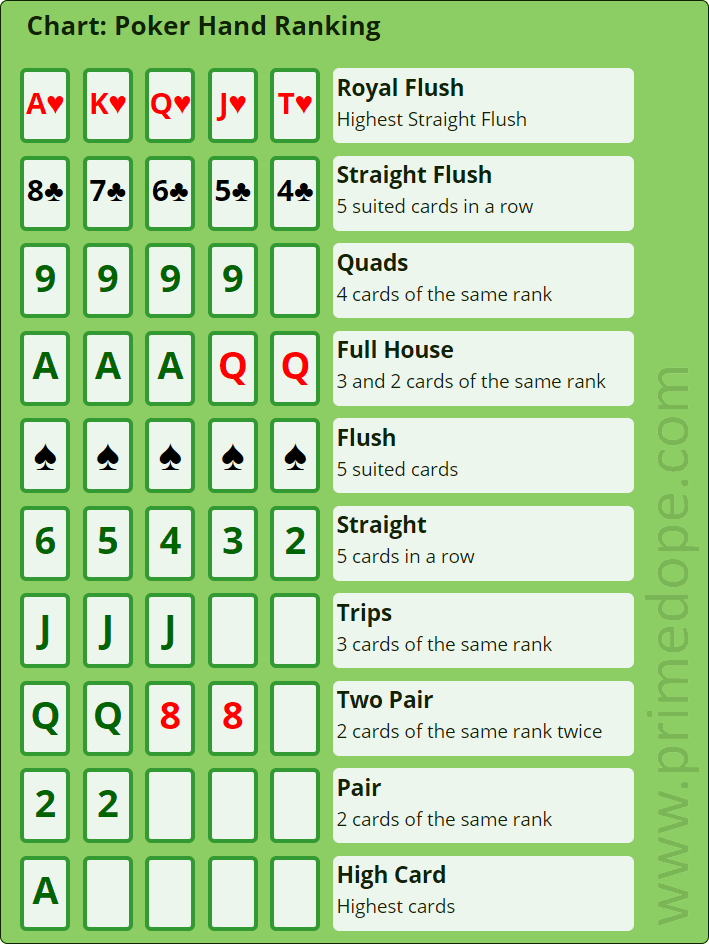
Poker hand rankings go from strongest to weakest:

1. Royal flush
2. Straight flush
3. Four of a kind
4. Full house
5. Flush
6. Straight
7. Three of a kind
8. Two pair
9. One pair
10. No pair (high card)

You can see that straight doesn’t beat a flush, but it does beat many other hands, making it a powerful hand on right boards. When the board is not paired, and no flush can be present, then if you hold the highest straight, you will have the best hand.

What are the odds of getting pocket aces?

Chances of being dealt pocket aces are slightly less than 0.5%. Exactly once every 221 hands, you will get the rockets. The number of players on the table doesn’t matter. There are still 52 cards in the deck, no matter how many players are at the table.

If you wonder how often you can expect to win with AA depending on the number of opponents and different hands you are up against, then read this post.

What are the odds of an ace flop?

We all know it, that horrible feeling when you hope ace doesn’t show up on the flop, but it seems like it always does. It doesn’t always come. But you will see ace on the flop 42% of the time, which is quite often. But don’t worry on some occasions you will also hit two flushes, sets or straights yourself. That is why pocket kings have around 70% (and not only 58%) to win against Ax.

POKER PROBABILITIES

• Texas Hold'em Poker
  Texas Hold'em Poker probabilities
• Omaha Poker
  Omaha Poker probabilities
• 5 Card Poker
  5 Card Poker probabilities

POKER CALCULATOR

• Poker calculator
  Poker odds calculator

POKER INFORMATION

• Poker hand rankings
  Ranking of poker hands

In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands.

Frequency of 5-card poker hands

The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement. Wild cards are not considered. The probability of drawing a given hand is calculated by dividing the number of ways of drawing the hand by the total number of 5-card hands (the sample space, five-card hands). The odds are defined as the ratio (1/p) - 1 : 1, where p is the probability. Note that the cumulative column contains the probability of being dealt that hand or any of the hands ranked higher than it. (The frequencies given are exact; the probabilities and odds are approximate.)

The nCr function on most scientific calculators can be used to calculate hand frequencies; entering ​nCr​ with ​52​ and ​5​, for example, yields as above.

Hand	Frequency	Approx. Probability	Approx. Cumulative	Approx. Odds	Mathematical expression of absolute frequency
Royal flush	4	0.000154%	0.000154%	649,739 : 1
Straight flush (excluding royal flush)	36	0.00139%	0.00154%	72,192.33 : 1
Four of a kind	624	0.0240%	0.0256%	4,164 : 1
Full house	3,744	0.144%	0.170%	693.2 : 1
Flush (excluding royal flush and straight flush)	5,108	0.197%	0.367%	507.8 : 1
Straight (excluding royal flush and straight flush)	10,200	0.392%	0.76%	253.8 : 1
Three of a kind	54,912	2.11%	2.87%	46.3 : 1
Two pair	123,552	4.75%	7.62%	20.03 : 1
One pair	1,098,240	42.3%	49.9%	1.36 : 1
No pair / High card	1,302,540	50.1%	100%	.995 : 1
Total	2,598,960	100%	100%	1 : 1

The royal flush is a case of the straight flush. It can be formed 4 ways (one for each suit), giving it a probability of 0.000154% and odds of 649,739 : 1.

When ace-low straights and ace-low straight flushes are not counted, the probabilities of each are reduced: straights and straight flushes each become 9/10 as common as they otherwise would be. The 4 missed straight flushes become flushes and the 1,020 missed straights become no pair.

Note that since suits have no relative value in poker, two hands can be considered identical if one hand can be transformed into the other by swapping suits. For example, the hand 3♣ 7♣ 8♣ Q♠ A♠ is identical to 3♦ 7♦ 8♦ Q♥ A♥ because replacing all of the clubs in the first hand with diamonds and all of the spades with hearts produces the second hand. So eliminating identical hands that ignore relative suit values, there are only 134,459 distinct hands.

The number of distinct poker hands is even smaller. For example, 3♣ 7♣ 8♣ Q♠ A♠ and 3♦ 7♣ 8♦ Q♥ A♥ are not identical hands when just ignoring suit assignments because one hand has three suits, while the other hand has only two—that difference could affect the relative value of each hand when there are more cards to come. However, even though the hands are not identical from that perspective, they still form equivalent poker hands because each hand is an A-Q-8-7-3 high card hand. There are 7,462 distinct poker hands.

Derivation of frequencies of 5-card poker hands

of the binomial coefficients and their interpretation as the number of ways of choosing elements from a given set. See also: sample space and event (probability theory).

• Straight flush — Each straight flush is uniquely determined by its highest ranking card; and these ranks go from 5 (A-2-3-4-5) up to A (10-J-Q-K-A) in each of the 4 suits. Thus, the total number of straight flushes is:
  • Royal straight flush — A royal straight flush is a subset of all straight flushes in which the ace is the highest card (ie 10-J-Q-K-A in any of the four suits). Thus, the total number of royal straight flushes is

    or simply . Note: this means that the total number of non-Royal straight flushes is 36.

• Four of a kind — Any one of the thirteen ranks can form the four of a kind by selecting all four of the suits in that rank. The final card can have any one of the twelve remaining ranks, and any suit. Thus, the total number of four-of-a-kinds is:

• Full house — The full house comprises a triple (three of a kind) and a pair. The triple can be any one of the thirteen ranks, and consists of three of the four suits. The pair can be any one of the remaining twelve ranks, and consists of two of the four suits. Thus, the total number of full houses is:

• Flush — The flush contains any five of the thirteen ranks, all of which belong to one of the four suits, minus the 40 straight flushes. Thus, the total number of flushes is:

Probability Of Getting A Straight Flush In 5 Card Poker

• Straight — The straight consists of any one of the ten possible sequences of five consecutive cards, from 5-4-3-2-A to A-K-Q-J-10. Each of these five cards can have any one of the four suits. Finally, as with the flush, the 40 straight flushes must be excluded, giving:

• Three of a kind — Any of the thirteen ranks can form the three of a kind, which can contain any three of the four suits. The remaining two cards can have any two of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of three-of-a-kinds is:

• Two pair — The pairs can have any two of the thirteen ranks, and each pair can have two of the four suits. The final card can have any one of the eleven remaining ranks, and any suit. Thus, the total number of two-pairs is:

• Pair — The pair can have any one of the thirteen ranks, and any two of the four suits. The remaining three cards can have any three of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of pair hands is:

• No pair — A no-pair hand contains five of the thirteen ranks, discounting the ten possible straights, and each card can have any of the four suits, discounting the four possible flushes. Alternatively, a no-pair hand is any hand that does not fall into one of the above categories; that is, any way to choose five out of 52 cards, discounting all of the above hands. Thus, the total number of no-pair hands is:

• Any five card poker hand — The total number of five card hands that can be drawn from a deck of cards is found using a combination selecting five cards, in any order where n refers to the number of items that can be selected and r to the sample size; the '!' is the factorial operator:

This guide is licensed under the GNU Free Documentation License. It uses material from the Wikipedia.

See Full List On En.wikipedia.org

Home > 5 Card Poker probabilities